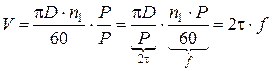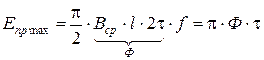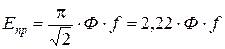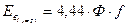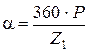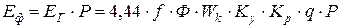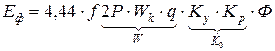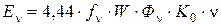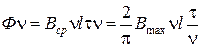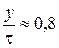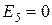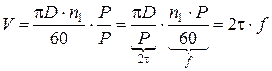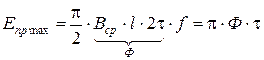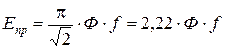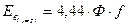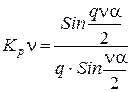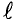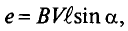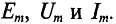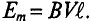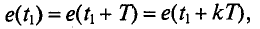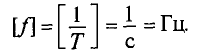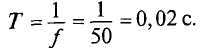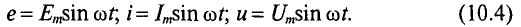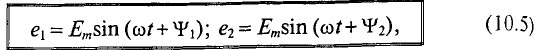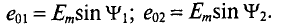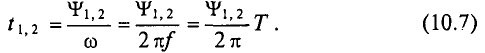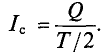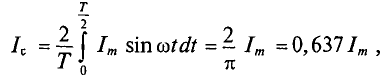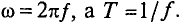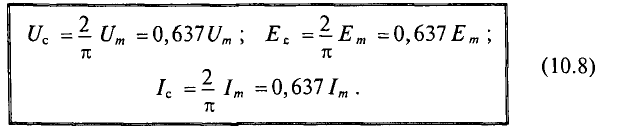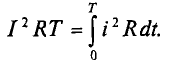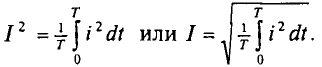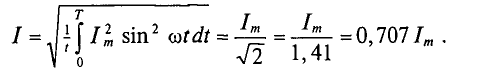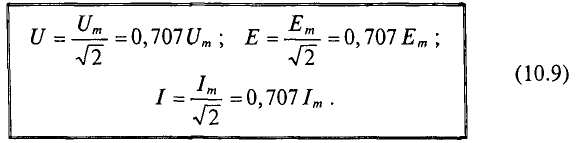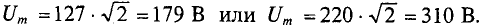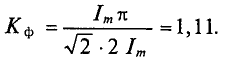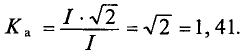Электродвижущая сила (ЭДС) обмотки машин переменного тока



Определим ЭДС проводника и витка с полным шагом y = t.
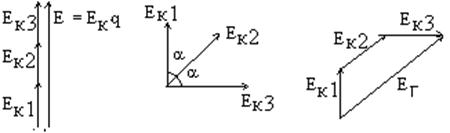
При этом, так как проводники находятся в одинаковых магнитных условиях, то ЭДС витка будет равна арифметической сумме (см. рис.).
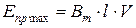
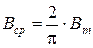
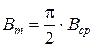
Действующее значение ЭДС проводника
2. ЭДС витка с полным шагом
3. ЭДС витка с укороченным шагом
Если виток имеет шаг y
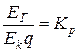
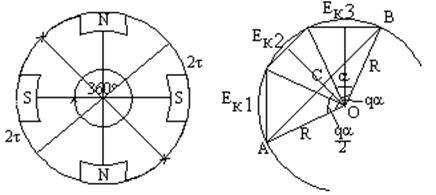
В электрической машине необходимо различать пространственный и электрический угол.
Пример. 2Р = 4, Р = 2 получим в одной пространственной окружности две электрических.
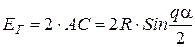
ЭДС катушки 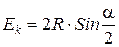
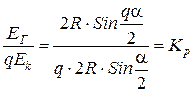
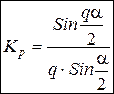
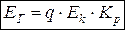
6. Определение ЭДС фазы.
Фаза состоит из нескольких катушечных групп, все катушечные группы расположены в одинаковых магнитных условиях, поэтому ЭДС фазы будет равна ЭДС катушечной группы умноженной на число их в фазе.
Если обмотка однослойная, то число катушечных групп в фазе равно числу пар полюсов – Р,
Если обмотка двухслойная, то число катушечных групп в фазе равно числу полюсов – 2Р
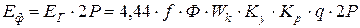
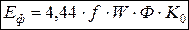
где W – число витков в фазе;
Ф – магнитный поток в веберах;
Ф×Ку – максимально сцепленный поток с катушкой.
Это выражение ЭДС фазы для первой гармоники.
ЭДС от высших гармоник потока
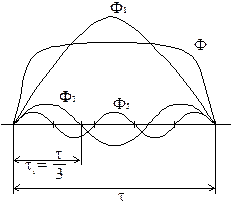
ЭДС от потока n гармоники запишется
полюсное деление 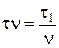
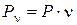
1. 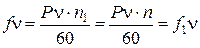
2.
3. 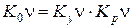
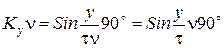
Если укорочение 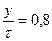
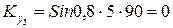
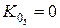
уменьшатся и 3 и 7 гармоники.
Пояснение, почему исчезает пятая гармоника ЭДС. Укорочение на 1/5t приводит к тому, что по контуру Е5 направлены встречно и их сумма равна 0.
Укорочение шага приводит к исчезновению пятой гармоники, третья гармоника уменьшается на половину, отсюда видно, что укорочение шага приводит к тому, что кривая ЭДС приближается к синусоиде и
он также меньше, чем для основной гармоники ЭДС.
Теперь можно подсчитать фазную ЭДС любой гармоники. Если обмотки соединены звездой, то в кривой линейных ЭДС – ЭДС кратным 3-м не будет. Если обмотки соединены в треугольник, то в линейных ЭДС их также не будет, т.к. они замкнутся по контуру.
Электродвижущая сила (ЭДС) обмотки машин переменного тока
Определим ЭДС проводника и витка с полным шагом y = t.
При этом, так как проводники находятся в одинаковых магнитных условиях, то ЭДС витка будет равна арифметической сумме (см. рис.).
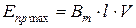
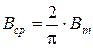
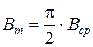
Действующее значение ЭДС проводника
2. ЭДС витка с полным шагом
3. ЭДС витка с укороченным шагом
Если виток имеет шаг y
он также меньше, чем для основной гармоники ЭДС.
Теперь можно подсчитать фазную ЭДС любой гармоники. Если обмотки соединены звездой, то в кривой линейных ЭДС – ЭДС кратным 3-м не будет. Если обмотки соединены в треугольник, то в линейных ЭДС их также не будет, т.к. они замкнутся по контуру.
Дата добавления: 2019-07-26 ; просмотров: 545 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Однофазные электрические цепи переменного тока
Содержание:
Однофазные электрические цепи переменного тока:
Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.
Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.
Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.
Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.
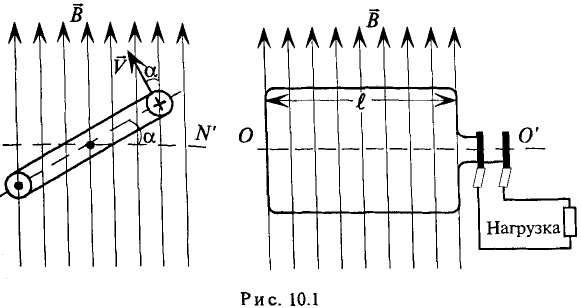
Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной
Плоскость 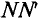
как 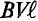
Синусоидальная ЭДС 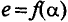
Величины, характеризующие синусоидальную ЭДС
Амплитуда — это максимальное значение периодически изменяющейся величины.
Обозначаются амплитуды прописными буквами с индексом m, т. е.
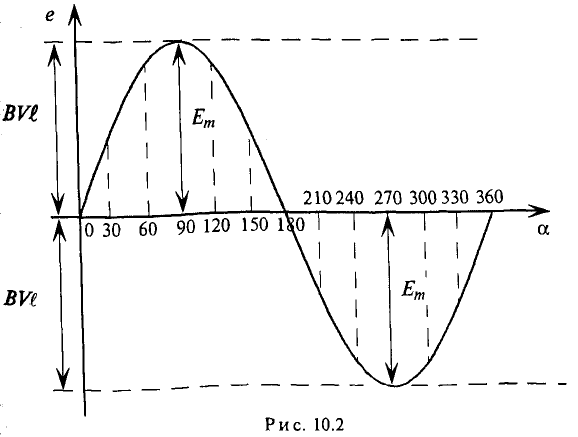
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол а = 90° или на угол а = 270°, так как 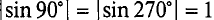
Тогда
Обозначается период буквой Т и измеряется в секундах, с (сек) т.е. 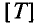
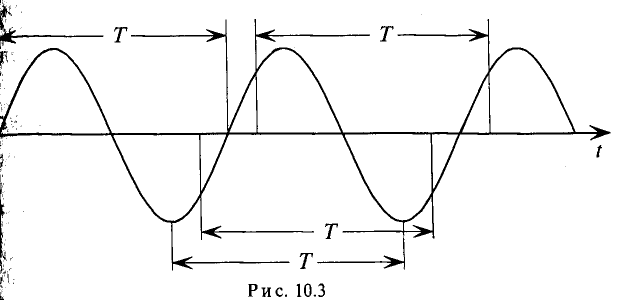
Значение ЭДС через каждый период определяется следующим равенством (рис. 10.3):
На рис. 10.3 изображена временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Обозначается частота буквой 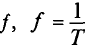
При частоте 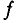
Угловая частота (угловая скорость) характеризуется углом поворотом рамки в единицу времени.
Обозначается угловая частота буквой 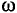
Измеряется угловая частота в единицах радиан в секунду, так как угол измеряется в радианах (рад).
Так, время одного периода Т рамка повернется на угол 360° = рад. Следовательно, угловую частоту можно выразить следующим образом:
Мгновенное значение — это значение переменной величины в й конкретный момент времени.
Мгновенные значения обозначаются строчными буквами..
Из выражения (10.2) следует, что угол поворота рамки 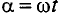
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Фаза и сдвиг фаз
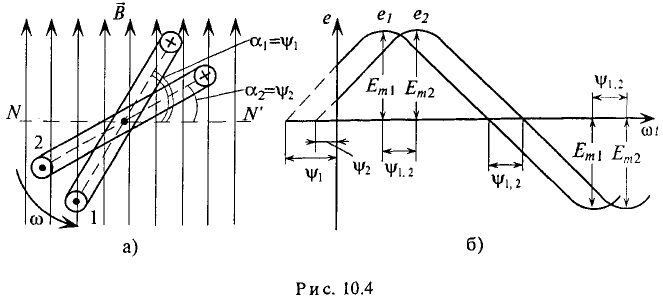
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а), т.е. амплитуды ЭДС 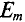
где 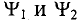
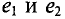
Поэтому эти углы 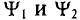
Начальные фазы 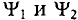
Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой 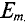

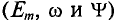


Величина 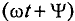
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:
При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. 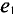
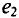
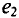
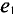
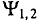
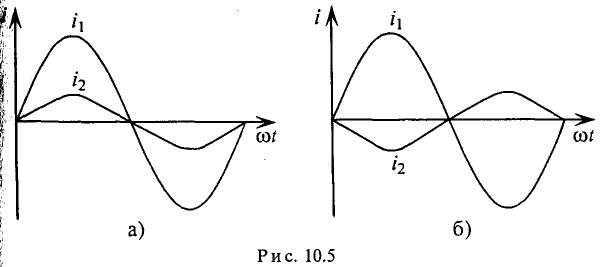
Две синусоидальные величины одинаковой частоты, достигаю-одновременно своих амплитудных (одного знака) и нулевых сечений, считаются совпадающими по фазе (рис. 10.5а).
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает и отстает от другой, характеризует время сдвига фаз 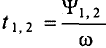
Среднее и действующее значения переменного тока
Кроме амплитудных и мгновенных значений переменный ток, напряжение, ЭДС характеризуются еще средними и действующими (эффективными) значениями.
Среднее значение переменного тока
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение провод-проходит то же количество электричества Q, что и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени.
Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. 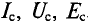
Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. 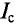
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
Из выражения (2.1) значение переменного тока 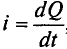
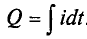
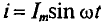
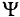
где
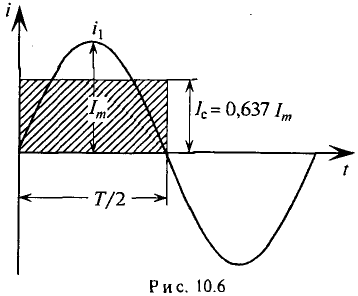
Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6).
Под средним значением переменной величины понимают постоянную составляющую этой величины.
Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
Действующее значение переменного тока
Действующее (или эффективное) значение переменного тока — значение переменного тока, эквивалентное постоянному току тепловому действию.
Действующее значения переменных величин обозначается прочими буквами без индексов: I, U, Е.
Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду первого тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток i:
Откуда действующее значение переменного тока
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е. 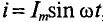
Номинальные значения тока и напряжения в электрических цепей и устройствах выражаются их действующими значениями.
Так, например, стандартные напряжения электрических сетей U= 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.
На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения.
Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Коэффициенты формы и амплитуды
Отклонения кривых тока, напряжения и ЭДС от синусоиды характеризуются коэффициентами формы 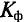
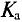
Коэффициент формы 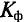
Коэффициент формы необходимо учитывать при проектировании и изучении выпрямительных устройств и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
Коэффициент амплитуды 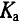
Для синусоидальных величин коэффициент амплитуды равен
Чем больше коэффициент формы и коэффициент амплитуды отличается от значений 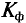
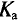
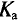
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.